Quick Overview
- For the function, $$f(x)$$, the average rate of change is denoted $$frac{Delta f}{Delta x}$$.
- In mathematics, the Greek letter $$Delta$$ (pronounced del-ta) means 'change'.
- When interpreting the average rate of change, we usually scale the result so that the denominator is 1.
- Average Rates of Change can be thought of as the slope of the line connecting two points on a function.
2.1 Average Rate of Change Notes 2.1 Key. Powered by Create your own unique website with customizable templates. Chapter 2.1: INSTANTANEOUS RATE OF CHANGE includes 23 full step-by-step solutions. Applied Calculus was written by and is associated to the ISBN: 920. This textbook survival guide was created for the textbook: Applied Calculus, edition: 5.
Familiar Example
Suppose you drive 120 miles in two hours. How fast were you going? The obvious answer is '60 miles per hour'.
Now, did you really drive at that speed the entire time? Maybe. Then again, you might have had to slow down because of heavy traffic for a while, but later you were able to drive a bit faster. So, over the two hours your speed averaged out to 60 mph.
This is called Average Velocity or Average Speed and it is a common example of using an average rate of change in our everyday lives.
Examples
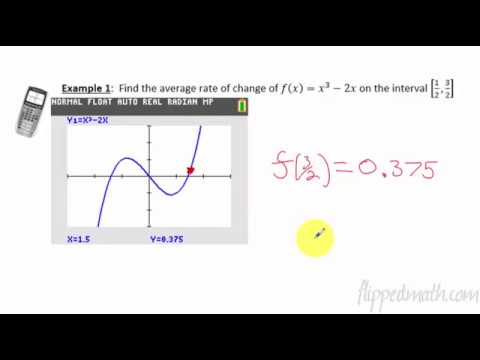
Example 1
Find the average rate of change for $$f(x) = x^2 -3x$$ between $$x = 1$$ and $$x = 6$$.
Step 1Calculate the change in function value.
$$ blue{f(6)}-red{f(1)} = blue{(6^2 -3cdot 6)} - red{(1^2 -3cdot 1)} = blue{18} - red{(-2)} = 20 $$
Step 2Calculate the change in the variable value.
$$ 6 -1 = 5 $$
Step 3Find the ratio of the changes.
$$ begin{align*} frac{Delta f}{Delta x} & = frac{f(6)-f(1)}{6 -1}[6pt] & = frac{20} 5[6pt] & = 4 end{align*} $$
AnswerThe average rate of change in $$f$$ between $$x = 1$$ and $$x = 6$$ is 4.
Example 2
Suppose the monthly profit for a particular company can be described by the function
$$P(x) = -x^2 + 9x - 8,$$
where $$x$$ is the number of tons of goods sold by the company and $$P(x)$$ is the amount of profit earned, measured in thousands of dollars.
Determine and interpret the value of $$frac{Delta P}{Delta x}$$ when the amount of goods sold increases from 4 tons to 4.5 tons.
Step 1Calculate $$frac{Delta P}{Delta x}$$
$$ begin{align*} frac{Delta P}{Delta x} & = frac{blue{P(4.5)} - red{P(4)}}{4.5 - 4}[6pt] & = frac{blue{(-(4.5)^2 + 9(4.5) - 8)} - red{(-(4)^2 + 9(4) - 8)}}{0.5}[6pt] & = frac{blue{12.25} - red{12}}{0.5}[6pt] & = frac{0.25}{0.5}[6pt] & = frac 1 2 end{align*} $$
Step 2Interpret the results.
We found that $$frac{Delta P}{Delta x} = frac{1/2} 1$$. This tells us that as sales increase from 4 to 4.5 tons, the profit will increase by $500 per ton on average.
Note: Since $$P(x)$$ is measured in thousands of dollars, $$Delta P = frac 1 2$$ means '1/2 of a thousand dollars,' which is $500.
Answer2.1 Average Rate Of Changeap Calculus Equation
As sales increase from 4 tons of goods to 4.5 tons of goods, we expect to see profits increase at an average rate of $500 per ton.
Example 3
Suppose an electrical circuit contains a variable resistor. As the resistor is adjusted from 3 ohms to 3.15 ohms, the electrical current is decreasing by an average 0.03 amps per ohm.
Write an equation that expresses this situation in terms of an average rate of change.
Step 1Define variables.
Let $$I =$$ the amount of current flowing through the circuit (measured in amps).
Let $$R=$$ the amount of resistance provided by the variable resistor (measured in ohms).
$$frac{Delta I}{Delta R} = -0.03$$
(Note that we are told in the statement of the problem what the average rate of change is. We're not asked to calculate it.)
Example 4
Suppose $$P$$ is measured in hundreds of fish and represents the size of a particular population of Hawaiian trigger fish, and $$t$$ represents time, measured in years. Interpret the following equation in a complete sentence.
$$ frac{Delta P}{Delta t} = 0.05 $$
Step 1Write the right-hand side of the equation as a fraction with a 1 in the denominator.
$$frac{Delta P}{Delta t} = frac{0.05} 1$$
Step 2Identify the values of $$Delta P$$ and $$Delta t$$.
$$Delta P = 0.05$$ which is the same as an increase of 5 fish, since $$P$$ is measured in hundreds of fish.
$$Delta t = 1$$ represents 1 year.
 Answer
AnswerThe population is increasing at an average rate of 5 fish per year.
Example 5
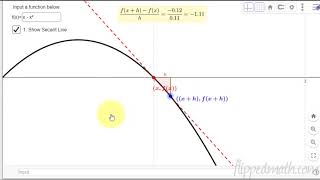
Suppose someone has been driving at exactly 60 miles per hour for one hour. How fast would they need to drive for the next 30 minutes in order to increase their average speed to 70 miles per hour?
Step 1Determine the total distanced traveled if the average speed were 70 mph for 1.5 hours.
$$ frac{70mbox{ miles}}{1 mbox{ hour}} cdot frac{1.5mbox{ hours}} 1 = 70(1.5)mbox{ miles} = 105mbox{ miles} $$
Step 2After traveling at 60mph for an hour, determine the remaining distance left to travel.
Since the driver has been driving at 60mph for one hour, the distance traveled so far is 60 miles. This leaves 45 miles to travel.
Step 3Determine the speed needed to cover 45 miles in 30 minutes.
$$ frac{45mbox{ miles}}{frac 1 2 mbox{ hour}} = frac{2cdot 45mbox{ miles}}{1mbox{ hour}} = frac{90mbox{ miles}}{1mbox{ hour}} $$
AnswerThe person would need to drive 90 miles per hour for 30 minutes.
2.1 Average Rate Of Changeap Calculus Ab
Continue to Practice Problems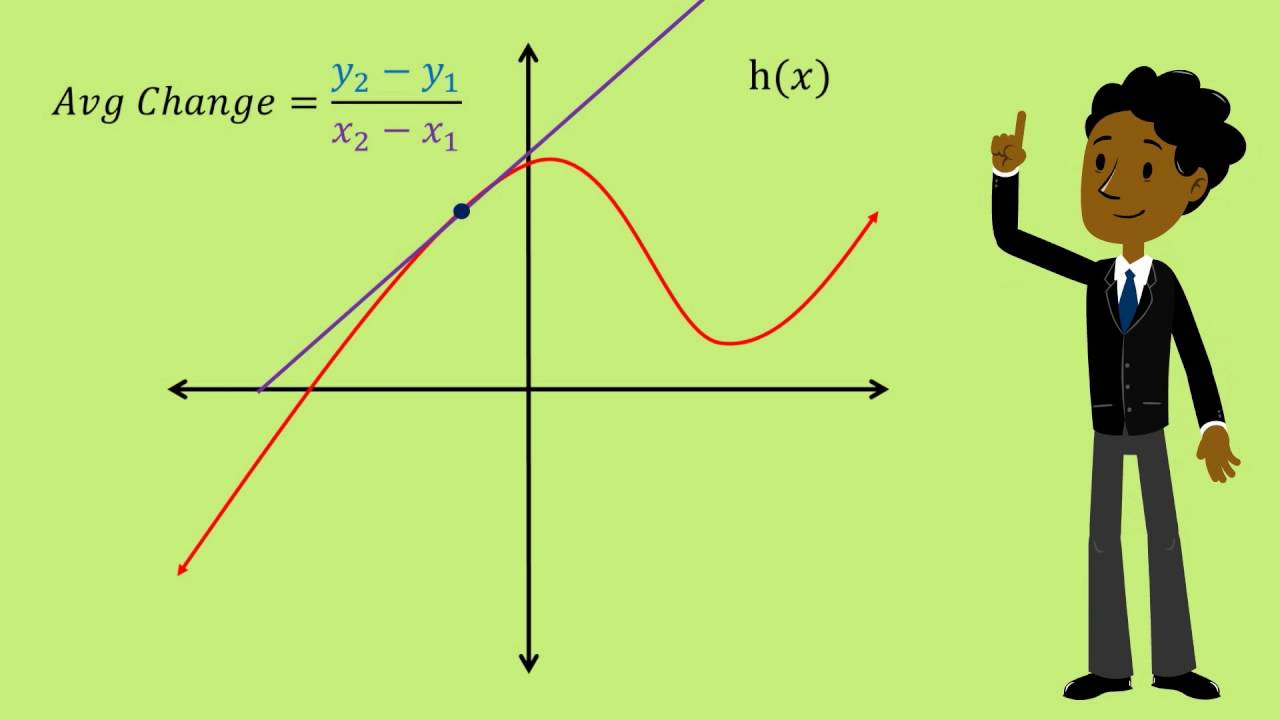
The calculator will find the average rate of change of the given function on the given interval, with steps shown.
- In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x`.
- In general, you can skip parentheses, but be very careful: e^3x is `e^3x`, and e^(3x) is `e^(3x)`.
- Also, be careful when you write fractions: 1/x^2 ln(x) is `1/x^2 ln(x)`, and 1/(x^2 ln(x)) is `1/(x^2 ln(x))`.
- If you skip parentheses or a multiplication sign, type at least a whitespace, i.e. write sin x (or even better sin(x)) instead of sinx.
- Sometimes I see expressions like tan^2xsec^3x: this will be parsed as `tan^(2*3)(x sec(x))`. To get `tan^2(x)sec^3(x)`, use parentheses: tan^2(x)sec^3(x).
- Similarly, tanxsec^3x will be parsed as `tan(xsec^3(x))`. To get `tan(x)sec^3(x)`, use parentheses: tan(x)sec^3(x).
- From the table below, you can notice that sech is not supported, but you can still enter it using the identity `sech(x)=1/cosh(x)`.
- If you get an error, double-check your expression, add parentheses and multiplication signs where needed, and consult the table below.
- All suggestions and improvements are welcome. Please leave them in comments.
2.1 Average Rate Of Changeap Calculus Formula
2.1 Average Rate Of Changeap Calculus Calculator
| Type | Get |
| Constants | |
| e | e |
| pi | `pi` |
| i | i (imaginary unit) |
| Operations | |
| a+b | a+b |
| a-b | a-b |
| a*b | `a*b` |
| a^b, a**b | `a^b` |
| sqrt(x), x^(1/2) | `sqrt(x)` |
| cbrt(x), x^(1/3) | `root(3)(x)` |
| root(x,n), x^(1/n) | `root(n)(x)` |
| x^(a/b) | `x^(a/b)` |
| x^a^b | `x^(a^b)` |
| abs(x) | `|x|` |
| Functions | |
| e^x | `e^x` |
| ln(x), log(x) | ln(x) |
| ln(x)/ln(a) | `log_a(x)` |
| Trigonometric Functions | |
| sin(x) | sin(x) |
| cos(x) | cos(x) |
| tan(x) | tan(x), tg(x) |
| cot(x) | cot(x), ctg(x) |
| sec(x) | sec(x) |
| csc(x) | csc(x), cosec(x) |
| Inverse Trigonometric Functions | |
| asin(x), arcsin(x), sin^-1(x) | asin(x) |
| acos(x), arccos(x), cos^-1(x) | acos(x) |
| atan(x), arctan(x), tan^-1(x) | atan(x) |
| acot(x), arccot(x), cot^-1(x) | acot(x) |
| asec(x), arcsec(x), sec^-1(x) | asec(x) |
| acsc(x), arccsc(x), csc^-1(x) | acsc(x) |
| Hyperbolic Functions | |
| sinh(x) | sinh(x) |
| cosh(x) | cosh(x) |
| tanh(x) | tanh(x) |
| coth(x) | coth(x) |
| 1/cosh(x) | sech(x) |
| 1/sinh(x) | csch(x) |
| Inverse Hyperbolic Functions | |
| asinh(x), arcsinh(x), sinh^-1(x) | asinh(x) |
| acosh(x), arccosh(x), cosh^-1(x) | acosh(x) |
| atanh(x), arctanh(x), tanh^-1(x) | atanh(x) |
| acoth(x), arccoth(x), cot^-1(x) | acoth(x) |
| acosh(1/x) | asech(x) |
| asinh(1/x) | acsch(x) |
